sum the total amount resulting from the addition of two or more numbers, amounts, or items sum to product and product to sum formulas tan the ratio of the opposite side to the adjacent side of a particular angle of the right triangle.. The sum-to-product formulas allow us to express sums of sine or cosine as products. These formulas can be derived from the product-to-sum identities. For example, with a few substitutions, we can derive the sum-to-product identity for sine. Let u + v 2 = α and u − v 2 = β.

Trigonometry Product to Sum & Sum to Product Formulas YouTube

Sum to Product Formulas for Sine and Cosine CK12 Foundation

Product of a Sum and a Difference YouTube

Product To Sum Formulas ListsDefinition, Formula, Example & Use

ProducttoSum and SumtoProduct Identities for Trigonometric Functions (Tagalog/Filipino Math

Factoring Trinomials using the SumProduct Method YouTube

PPT CHAPTER 5 PowerPoint Presentation, free download ID583237

Solved (5). ( Product to Sum and Sum to Product

PPT Chapter 5 Verifying Trigonometric Identities PowerPoint Presentation ID1294850

Sum and Product Formulas YouTube

Precalc 5.5 Multiple Angle and Product to Sum Formulas YouTube

Solved Use a SumtoProduct Formula to show the following.

Question 2 Find a cubic polynomial with sum, product Difficult Pol

PPT DoubleAngle, HalfAngle, and ProductSum Formulas PowerPoint Presentation ID9714468

155 24a SumProduct and ProductSum formulas YouTube

PPT Section 7.3 DoubleAngle, HalfAngle and ProductSum Formulas PowerPoint Presentation ID

Product to Sum and Sum to Product Formulas YouTube
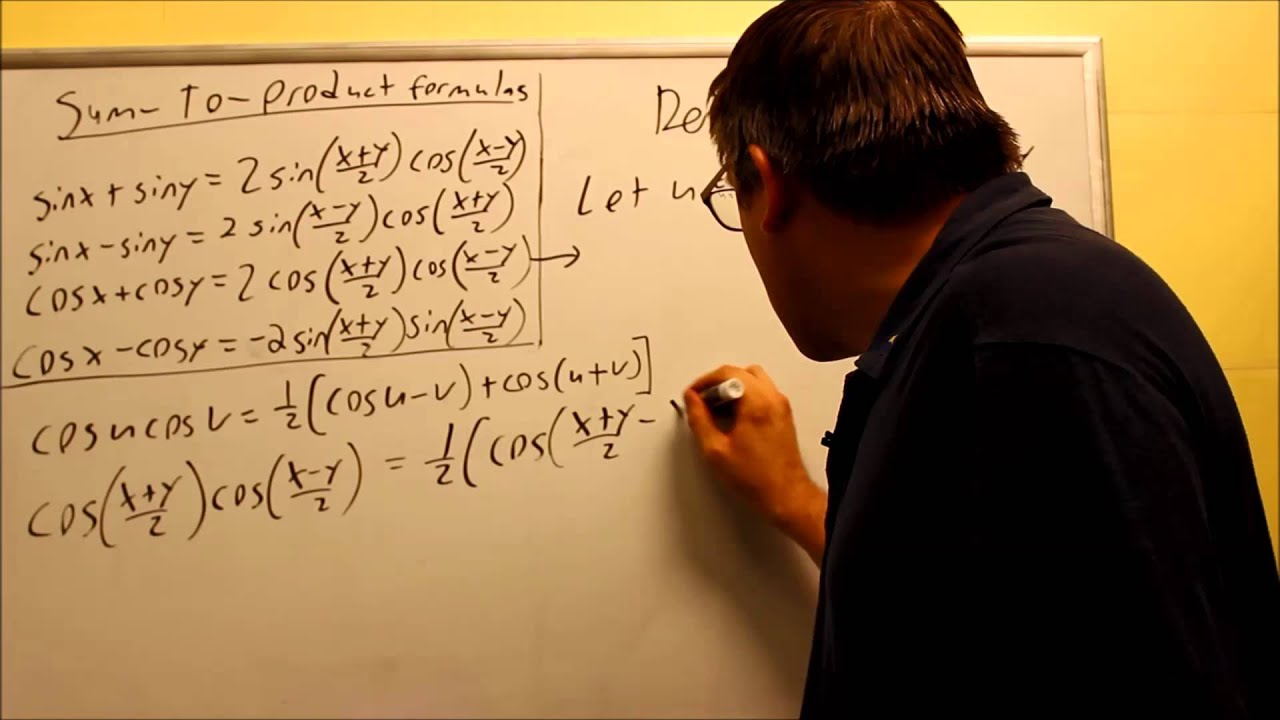
SumToProduct Formulas (Intro) and Derivation YouTube

Product To Sum Identities and Sum To Product Formulas Trigonometry YouTube

Productsum method Solving quadratic equations YouTube
We can use the product-to-sum formulas, which express products of trigonometric functions as sums. Let’s investigate the cosine identity first and then the sine identity. Expressing Products as Sums for Cosine. We can derive the product-to-sum formula from the sum and difference identities for cosine. If we add the two equations, we get:. We can use the product-to-sum formulas, which express products of trigonometric functions as sums. Let’s investigate the cosine identity first and then the sine identity. Expressing Products as Sums for Cosine. We can derive the product-to-sum formula from the sum and difference identities for cosine. If we add the two equations, we get: